初中名师视频课程免费试听1200分钟 |
||||
| 初一全科强化班辅导课程 免费听课 | 初二强化班辅导课程 免费听课 | 初三强化班辅导课程 免费听课 | ||
二次函数交点与二次方程根的关系:
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1、若△>0,则一元二次方程ax2+bx+c=0有两个不等的实数根,则抛物线y=ax2+bx+c与x轴有两个交点---相交;
2、若△=0,则一元二次方程ax2+bx+c=0有两个相等的实数根,则抛物线y=ax2+bx+c与x轴有唯一公共点---相切(顶点);
3、若△<0,则一元二次方程ax2+bx+c=0没有实数根,则抛物线y=ax2+bx+c与x轴没有公共点--相离。
若抛物线y=ax2+bx+c与轴的两个交点坐标分别是A(x1,0),B(x2,0),则x1+x2=-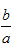 ,x1x2=
,x1x2=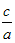

向上吧同学
扫描二维码获取学习资料